2. Getting Started¶
Here, we explain how to use ABCpy to quantify parameter uncertainty of a probabilistic model given some observed dataset. If you are new to uncertainty quantification using Approximate Bayesian Computation (ABC), we recommend you to start with the Parameters as Random Variables section.
Moreover, we also provide an interactive notebook on Binder guiding through the basics of ABC with ABCpy; without installing that on your machine. Please find it here.
Parameters as Random Variables¶
As an example, if we have measurements of the height of a group of grown up humans and it is also known that a Gaussian distribution is an appropriate probabilistic model for these kind of observations, then our observed dataset would be measurement of heights and the probabilistic model would be Gaussian.
# define observation for true parameters mean=170, std=15
height_obs = [160.82499176, 167.24266737, 185.71695756, 153.7045709, 163.40568812, 140.70658699, 169.59102084,
172.81041696, 187.38782738, 179.66358934, 176.63417241, 189.16082803, 181.98288443, 170.18565017,
183.78493886, 166.58387299, 161.9521899, 155.69213073, 156.17867343, 144.51580379, 170.29847515,
197.96767899, 153.36646527, 162.22710198, 158.70012047, 178.53470703, 170.77697743, 164.31392633,
165.88595994, 177.38083686, 146.67058471763457, 179.41946565658628, 238.02751620619537,
206.22458790620766, 220.89530574344568, 221.04082532837026, 142.25301427453394, 261.37656571434275,
171.63761180867033, 210.28121820385866, 237.29130237612236, 175.75558340169619, 224.54340549862235,
197.42448680731226, 165.88273684581381, 166.55094082844519, 229.54308602661584, 222.99844054358519,
185.30223966014586, 152.69149367593846, 206.94372818527413, 256.35498655339154, 165.43140916577741,
250.19273595481803, 148.87781549665536, 223.05547559193792, 230.03418198709608, 146.13611923127021,
138.24716809523139, 179.26755740864527, 141.21704876815426, 170.89587081800852, 222.96391329259626,
188.27229523693822, 202.67075179617672, 211.75963110985992, 217.45423324370509]
# define the model
from abcpy.continuousmodels import Normal as Gaussian
height = Gaussian([mu, sigma], name='height')
The Gaussian or Normal model has two parameters: the mean, denoted by \(\mu\), and the standard deviation, denoted by \(\sigma\). We consider these parameters as random variables. The goal of ABC is to quantify the uncertainty of these parameters from the information contained in the observed data.
In ABCpy, a abcpy.probabilisticmodels.ProbabilisticModel object represents probabilistic relationship
between random variables or between random variables and observed data. Each of the ProbabilisticModel object has a number of input parameters: they are either random
variables (output of another ProbabilisticModel object) or
constant values and considered known to the user (Hyperparameters). If you are interested in implementing your own probabilistic model,
please check the implementing a new model section.
To define a parameter of a model as a random variable, you start by assigning a prior distribution on them. We can utilize prior knowledge about these parameters as prior distribution. In the absence of prior knowledge, we still need to provide prior information and a non-informative flat distribution on the parameter space can be used. The prior distribution on the random variables are assigned by a probabilistic model which can take other random variables or hyper parameters as input.
In our Gaussian example, providing prior information is quite simple. We know from experience that the average height should be somewhere between 150cm and 200cm, while the standard deviation is around 5 to 25. In code, this would look as follows:
# define prior
from abcpy.continuousmodels import Uniform
mu = Uniform([[150], [200]], name="mu")
sigma = Uniform([[5], [25]], name="sigma")
# define the model
from abcpy.continuousmodels import Normal as Gaussian
height = Gaussian([mu, sigma], name='height')
We have defined the parameter \(\mu\) and \(\sigma\) of the Gaussian model as random variables and assigned
Uniform prior distributions on them. The parameters of the prior distribution \((150, 200, 5, 25)\) are assumed to
be known to the user, hence they are called hyperparameters. Also, internally, the hyperparameters are converted to
Hyperparameter objects. Note that you are also required to pass
a name string while defining a random variable. In the final output, you will see these names, together with the
relevant outputs corresponding to them.
For uncertainty quantification, we follow the philosophy of Bayesian inference. We are interested in the distribution of the parameters we get after incorporating the information that is implicit in the observed dataset with the prior information. This target distribution is called posterior distribution of the parameters. For inference, we draw independent and identical sample values from the posterior distribution. These sampled values are called posterior samples and used to either approximate the posterior distribution or to integrate in a Monte Carlo style w.r.t the posterior distribution. The posterior samples are the ones you get as a result of applying an ABC inference scheme.
The heart of the ABC inferential algorithm is a measure of discrepancy between the observed dataset and the synthetic dataset (simulated/generated from the model). Often, computation of discrepancy measure between the observed and synthetic dataset is not feasible (e.g., high dimensionality of dataset, computationally to complex) and the discrepancy measure is defined by computing a distance between relevant summary statistics extracted from the datasets. Here we first define a way to extract summary statistics from the dataset.
# define statistics
from abcpy.statistics import Identity
statistics_calculator = Identity(degree=2, cross=False)
Next we define the discrepancy measure between the datasets, by defining a distance function (LogReg distance is chosen here) between the extracted summary statistics. If we want to define the discrepancy measure through a distance function between the datasets directly, we choose Identity as summary statistics which gives the original dataset as the extracted summary statistics. This essentially means that the distance object automatically extracts the statistics from the datasets, and then compute the distance between the two statistics.
# define distance
from abcpy.distances import LogReg
distance_calculator = LogReg(statistics_calculator, seed=42)
Algorithms in ABCpy often require a perturbation kernel, a tool to explore the parameter space. Here, we use the default kernel provided, which explores the parameter space of random variables, by using e.g. a multivariate Gaussian distribution or by performing a random walk depending on whether the corresponding random variable is continuous or discrete. For a more involved example, please consult Composite Perturbation Kernels.
# define kernel
from abcpy.perturbationkernel import DefaultKernel
kernel = DefaultKernel([mu, sigma])
Finally, we need to specify a backend that determines the parallelization framework to use. The example code here uses
the dummy backend BackendDummy which does not parallelize the computation of the
inference schemes, but which is handy for prototyping and testing. For more advanced parallelization backends
available in ABCpy, please consult Using Parallelization Backends section.
# define backend
# Note, the dummy backend does not parallelize the code!
from abcpy.backends import BackendDummy as Backend
backend = Backend()
In this example, we choose PMCABC algorithm (inference scheme) to draw posterior samples of the parameters. Therefore, we instantiate a PMCABC object by passing the random variable corresponding to the observed dataset, the distance function, backend object, perturbation kernel and a seed for the random number generator.
# define sampling scheme
from abcpy.inferences import PMCABC
sampler = PMCABC([height], [distance_calculator], backend, kernel, seed=1)
Finally, we can parametrize the sampler and start sampling from the posterior distribution of the parameters given the observed dataset:
# sample from scheme
eps_arr = np.array([.75])
epsilon_percentile = 10
journal = sampler.sample([height_obs], steps, eps_arr, n_sample, n_samples_per_param, epsilon_percentile)
The above inference scheme gives us samples from the posterior distribution of the parameter of interest height quantifying the uncertainty of the inferred parameter, which are stored in the journal object. See Post Analysis for further information on extracting results.
Note that the model and the observations are given as a list. This is due to the fact that in ABCpy, it is possible to have hierarchical models, building relationships between co-occurring groups of datasets. To learn more, see the Hierarchical Model section.
The full source can be found in examples/extensions/models/gaussian_python/pmcabc_gaussian_model_simple.py. To execute the code you only need to run
python3 pmcabc_gaussian_model_simple.py
Probabilistic Dependency between Random Variables¶
Since release 0.5.0 of ABCpy, a probabilistic dependency structures (e.g., a Bayesian network) between random variables can be modelled. Behind the scene, ABCpy will represent this dependency structure as a directed acyclic graph (DAG) such that the inference can be done on the full graph. Further we can also define new random variables through operations between existing random variables. To make this concept more approachable, we now exemplify an inference problem on a probabilistic dependency structure.
Students of a school took an exam and received some grade. The observed grades of the students are:
grades_obs = [3.872486707973337, 4.6735380808674405, 3.9703538990858376, 4.11021272048805, 4.211048655421368,
4.154817956586653, 4.0046893064392695, 4.01891381384729, 4.123804757702919, 4.014941267301294,
3.888174595940634, 4.185275142948246, 4.55148774469135, 3.8954427675259016, 4.229264035335705,
3.839949451328312, 4.039402553532825, 4.128077814241238, 4.361488645531874, 4.086279074446419,
4.370801602256129, 3.7431697332475466, 4.459454162392378, 3.8873973643008255, 4.302566721487124,
4.05556051626865, 4.128817316703757, 3.8673704442215984, 4.2174459453805015, 4.202280254493361,
4.072851400451234, 3.795173229398952, 4.310702877332585, 4.376886328810306, 4.183704734748868,
4.332192463368128, 3.9071312388426587, 4.311681374107893, 3.55187913252144, 3.318878360783221,
4.187850500877817, 4.207923106081567, 4.190462065625179, 4.2341474252986036, 4.110228694304768,
4.1589891480847765, 4.0345604687633045, 4.090635481715123, 3.1384654393449294, 4.20375641386518,
4.150452690356067, 4.015304457401275, 3.9635442007388195, 4.075915739179875, 3.5702080541929284,
4.722333310410388, 3.9087618197155227, 4.3990088006390735, 3.968501165774181, 4.047603645360087,
4.109184340976979, 4.132424805281853, 4.444358334346812, 4.097211737683927, 4.288553086265748,
3.8668863066511303, 3.8837108501541007]
which depend on several variables: if there were bias, the average size of the classes, as well as the number of teachers at the school. Here we assume the average size of a class and the number of the teachers at the school are normally distributed with some mean, depending on the budget of the school and variance $1$. We further assume that the budget of the school is uniformly distributed between 1 and 10 millions US dollars. Finally, we can assume that the grade without any bias would be a normally distributed parameter around an average grade. The dependency structure between these variables can be defined using the following Bayesian network:
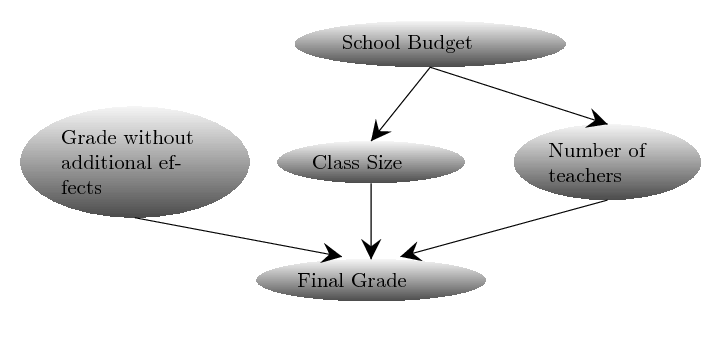
We can define these random variables and the dependencies between them in ABCpy in the following way:
from abcpy.continuousmodels import Uniform, Normal
school_budget = Uniform([[1], [10]], name='school_budget')
class_size = Normal([[800 * school_budget], [1]], name='class_size')
no_teacher = Normal([[20 * school_budget], [1]], name='no_teacher')
grade_without_additional_effects = Normal([[4.5], [0.25]], name='grade_without_additional_effects')
So, each student will receive some grade without additional effects which is normally distributed, but then the final grade recieved will be a function of grade without additional effects and the other random variables defined beforehand (e.g., school_budget, class_size and no_teacher). The model for the final grade of the students now can be written as:
final_grade = grade_without_additional_effects - .001 * class_size + .02 * no_teacher
Notice here we created a new random variable final_grade, by subtracting the random variables class_size multiplied
by 0.001 and adding no_teacher multiplied by 0.02 from the random variable grade_without_additional_effects.
In short, this illustrates that you can perform standard operations “+”,
“-”, “*”, “/” and “**” (the power operator in Python) on any two random variables, to get a new random variable. It is
possible to perform these operations between two random variables additionally to the general data types of Python
(integer, float, and so on) since they are converted to HyperParameters.
Please keep in mind that parameters defined via operations will not be included in your list of parameters in the
journal file. However, all parameters that are part of the operation, and are not fixed, will be included, so you can
easily perform the required operations on the final result to get these parameters, if necessary. In addition, you can
now also use the [] operator (the access operator in Python). This allows you to select single values or ranges
of a multidimensional random variable as a parameter of a new random variable.
Hierarchical Model¶
ABCpy also supports inference when co-occurring datasets are available. To illustrate how this is implemented, we will consider the example from Probabilistic Dependency between Random Variables section and extend it for co-occurring datasets, when we also have data for final scholarships given out by the school to the students in addition to the final grade of a student.

Whether a student gets a scholarship depends on the number of teachers in the school and on an independent score. Assuming the score is normally distributed, we can model the impact of the students social background on the scholarship as follows:
scholarship_obs = [2.7179657436207805, 2.124647285937229, 3.07193407853297, 2.335024761813643, 2.871893855192,
3.4332002458233837, 3.649996835818173, 3.50292335102711, 2.815638168018455, 2.3581613289315992,
2.2794821846395568, 2.8725835459926503, 3.5588573782815685, 2.26053126526137, 1.8998143530749971,
2.101110815311782, 2.3482974964831573, 2.2707679029919206, 2.4624550491079225, 2.867017757972507,
3.204249152084959, 2.4489542437714213, 1.875415915801106, 2.5604889644872433, 3.891985093269989,
2.7233633223405205, 2.2861070389383533, 2.9758813233490082, 3.1183403287267755,
2.911814060853062, 2.60896794303205, 3.5717098647480316, 3.3355752461779824, 1.99172284546858,
2.339937680892163, 2.9835630207301636, 2.1684912355975774, 3.014847335983034, 2.7844122961916202,
2.752119871525148, 2.1567428931391635, 2.5803629307680644, 2.7326646074552103, 2.559237193255186,
3.13478196958166, 2.388760269933492, 3.2822443541491815, 2.0114405441787437, 3.0380056368041073,
2.4889680313769724, 2.821660164621084, 3.343985964873723, 3.1866861970287808, 4.4535037154856045,
3.0026333138006027, 2.0675706089352612, 2.3835301730913185, 2.584208398359566, 3.288077633446465,
2.6955853384148183, 2.918315169739928, 3.2464814419322985, 2.1601516779909433, 3.231003347780546,
1.0893224045062178, 0.8032302688764734, 2.868438615047827]
scholarship_without_additional_effects = Normal([[2], [0.5]], name='schol_without_additional_effects')
final_scholarship = scholarship_without_additional_effects + .03 * no_teacher
With this we now have two root ProbabilisicModels (random variables), namely final_grade and
final_scholarship, whose output can directly compared to the observed datasets grade_obs and
scholarship_obs. With this we are able to do an inference computation on all free parameters of the hierarchical
model (of the DAG) given our observations.
To infer uncertainty of our parameters, we follow the same steps as in our previous examples: We choose summary statistics, distance, inference scheme, backend and kernel. We will skip the definitions that have not changed from the previous section. However, we would like to point out the difference in definition of the distance. Since we are now considering two observed datasets, we need to define a distance on each one of them separately. Here, we use the Euclidean distance for each observed data set and corresponding simulated dataset. You can use two different distances on two different observed datasets.
# Define a summary statistics for final grade and final scholarship
from abcpy.statistics import Identity
statistics_calculator_final_grade = Identity(degree=2, cross=False)
statistics_calculator_final_scholarship = Identity(degree=3, cross=False)
# Define a distance measure for final grade and final scholarship
from abcpy.distances import Euclidean
distance_calculator_final_grade = Euclidean(statistics_calculator_final_grade)
distance_calculator_final_scholarship = Euclidean(statistics_calculator_final_scholarship)
Using these two distance functions with the final code look as follows:
# Define a backend
from abcpy.backends import BackendDummy as Backend
backend = Backend()
# Define a perturbation kernel
from abcpy.perturbationkernel import DefaultKernel
kernel = DefaultKernel([school_budget, class_size, grade_without_additional_effects,
no_teacher, scholarship_without_additional_effects])
eps_arr = np.array([30]) # starting value of epsilon; the smaller, the slower the algorithm.
# at each iteration, take as epsilon the epsilon_percentile of the distances obtained by simulations at previous
# iteration from the observation
epsilon_percentile = 10
# Define sampler; note here how the two models are passed in a list, as well as the two corresponding distance
# calculators
from abcpy.inferences import PMCABC
sampler = PMCABC([final_grade, final_scholarship],
[distance_calculator_final_grade, distance_calculator_final_scholarship], backend, kernel, seed=1)
# Sample; again, here we pass the two sets of observations in a list
journal = sampler.sample([grades_obs, scholarship_obs],
steps, eps_arr, n_sample, n_samples_per_param, epsilon_percentile)
Observe that the lists given to the sampler and the sampling method now contain two entries. These correspond to the two different observed data sets respectively. Also notice now we provide two different distances corresponding to the two different root models and their observed datasets. Presently ABCpy combines the distances by a linear combination, however customized combination strategies can be implemented by the user.
The full source code can be found in examples/hierarchicalmodels/pmcabc_inference_on_multiple_sets_of_obs.py.
Composite Perturbation Kernels¶
As pointed out earlier, it is possible to define composite perturbation kernels, perturbing different random variables in different ways. Let us take the same example as in the Hierarchical Model and assume that we want to perturb the schools budget, grade score and scholarship score without additional effect, using a multivariate normal kernel. However, the remaining parameters we would like to perturb using a multivariate Student’s-T kernel. This can be implemented as follows:
from abcpy.perturbationkernel import MultivariateNormalKernel, MultivariateStudentTKernel
kernel_1 = MultivariateNormalKernel(
[school_budget, scholarship_without_additional_effects, grade_without_additional_effects])
kernel_2 = MultivariateStudentTKernel([class_size, no_teacher], df=3)
We have now defined how each set of parameters is perturbed on its own. The sampler object, however, needs to be
provided with one single kernel. We, therefore, provide a class which groups the above kernels together. This class,
abcpy.perturbationkernel.JointPerturbationKernel, knows how to perturb each set of parameters individually.
It just needs to be provided with all the relevant kernels:
# Join the defined kernels
from abcpy.perturbationkernel import JointPerturbationKernel
kernel = JointPerturbationKernel([kernel_1, kernel_2])
This is all that needs to be changed. The rest of the implementation works the exact same as in the previous example. If you would like to implement your own perturbation kernel, please check Implementing a new Perturbation Kernel. Please keep in mind that you can only perturb parameters. You cannot use the access operator to perturb one component of a multi-dimensional random variable differently than another component of the same variable.
The source code to this section can be found in examples/extensions/perturbationkernels/pmcabc_perturbation_kernels.py.
Inference Schemes¶
In ABCpy, we implement widely used and advanced variants of ABC inferential schemes:
- Rejection ABC
abcpy.inferences.RejectionABC, - Population Monte Carlo ABC
abcpy.inferences.PMCABC, - Two versions of Sequential Monte Carlo ABC
abcpy.inferences.SMCABC, - Replenishment sequential Monte Carlo ABC (RSMC-ABC)
abcpy.inferences.RSMCABC, - Adaptive population Monte Carlo ABC (APMC-ABC)
abcpy.inferences.APMCABC, - ABC with subset simulation (ABCsubsim)
abcpy.inferences.ABCsubsim, and - Simulated annealing ABC (SABC)
abcpy.inferences.SABC.
To perform ABC algorithms, we provide different the standard Euclidean distance function
(abcpy.distances.Euclidean) as well as discrepancy measures between empirical datasets
(eg, achievable classification accuracy between two datasets
- classification accuracy (
abcpy.distances.LogReg,abcpy.distances.PenLogReg) abcpy.distances.Wassersteinabcpy.distances.SlicedWassersteinabcpy.distances.GammaDivergenceabcpy.distances.KLDivergenceabcpy.distances.MMDabcpy.distances.EnergyDistanceabcpy.distances.SquaredHellingerDistance.
We also have implemented the standard Metropolis-Hastings MCMC abcpy.inferences.MCMCMetropoliHastings and population Monte Carlo abcpy.inferences.PMC algorithm to infer parameters when
the likelihood or approximate likelihood function is available. For approximation of the likelihood function we provide
the following methods methods:
- Synthetic likelihood approximation
abcpy.approx_lhd.SynLikelihood, - Semiparametric Synthetic likelihood
abcpy.approx_lhd.SemiParametricSynLikelihood, and another method using - penalized logistic regression
abcpy.approx_lhd.PenLogReg.
Finally, we also include a utility class with a similar API as the previous inference schemes which allows to sample from the prior: abcpy.inferences.DrawFromPrior.
Next we explain how we can use PMC algorithm using approximation of the
likelihood functions. As we are now considering two observed datasets
corresponding to two root models, we need to define an approximation of
likelihood function for each of them separately. Here, we use the
abcpy.approx_lhd.SynLikelihood for each of the root models. It is
also possible to use two different approximate likelihoods for two different
root models.
# Define a summary statistics for final grade and final scholarship
from abcpy.statistics import Identity
statistics_calculator_final_grade = Identity(degree=2, cross=False)
statistics_calculator_final_scholarship = Identity(degree=3, cross=False)
# Define an approximate likelihood for final grade and final scholarship
from abcpy.approx_lhd import SynLikelihood
approx_lhd_final_grade = SynLikelihood(statistics_calculator_final_grade)
approx_lhd_final_scholarship = SynLikelihood(statistics_calculator_final_scholarship)
We then parametrize the sampler and sample from the posterior distribution.
# Define sampler to use with the
from abcpy.inferences import PMC
sampler = PMC([final_grade, final_scholarship],
[approx_lhd_final_grade, approx_lhd_final_scholarship], backend, kernel, seed=1)
# Sample
journal = sampler.sample([grades_obs, scholarship_obs], steps, n_sample, n_samples_per_param)
Observe that the lists given to the sampler and the sampling method now contain two entries. These correspond to the two different observed data sets respectively. Also notice we now provide two different distances corresponding to the two different root models and their observed datasets. Presently ABCpy combines the distances by a linear combination. Further possibilities of combination will be made available in later versions of ABCpy.
The source code can be found in examples/approx_lhd/pmc_hierarchical_models.py.
For an example using MCMC instead of PMC, check out examples/approx_lhd/mcmc_hierarchical_models.py.
Statistics Learning¶
As we have discussed in the Parameters as Random Variables Section, the discrepancy measure between two datasets is
defined by a distance function between extracted summary statistics from the datasets. Hence, the ABC algorithms are
subjective to the summary statistics choice. This subjectivity can be avoided by a data-driven summary statistics choice
from the available summary statistics of the dataset. In ABCpy we provide several statistics learning procedures,
implemented in the subclasses of abcpy.statisticslearning.StatisticsLearning, that generate a training
dataset of (parameter, sample) pairs and use it to learn a transformation of the data that will be used in the inference
step. The following techniques are available:
- Semiautomatic
abcpy.statisticslearning.Semiautomatic, - SemiautomaticNN
abcpy.statisticslearning.SemiautomaticNN, - ContrastiveDistanceLearning
abcpy.statisticslearning.ContrastiveDistanceLearning, - TripletDistanceLearning
abcpy.statisticslearning.TripletDistanceLearning. - ExponentialFamilyScoreMatching
abcpy.statisticslearning.ExponentialFamilyScoreMatching.
The first two build a transformation that approximates the parameter that generated the corresponding observation, the first one by using a linear regression approach and the second one by using a neural network embedding. The two distance learning approaches use instead neural networks to learn an embedding of the data so that the distance between the embeddings is close to the distance between the parameter values that generated the data. Finally, the last one fits an exponential family approximation to the likelihood using the generated data, and uses as summary statistics the sufficient statistics of the approximating family. Two neural networks are used here in the training phase, one to learn the summary statistics and one to transform the parameters to the natural parametrization of the learned exponential family (but only the second neural network will be used when the statistics are used in inference).
We remark that the techniques using neural networks require Pytorch to be installed. As this is an optional feature, however, Pytorch is not in the list of dependencies of ABCpy. Rather, when one of the neural network based routines is called, ABCpy checks if Pytorch is present and, if not, asks the user to install it. Moreover, unless the user wants to provide a specific form of neural network, the implementation of the neural network based ones do not require any explicit neural network coding, handling all the necessary definitions and training internally.
It is also possible to provide a validation set to the neural network based training routines in order to monitor the
loss on fresh samples. This can be done for instance by set the parameter n_samples_val to a value larger than 0.
Moreover, it is possible to use the validation set for early stopping, ie stopping the training as soon as the loss on
the validation set starts increasing. You can do this by setting early_stopping=True. Please refer to the API documentation
(for instance abcpy.statisticslearning.SemiautomaticNN) for further details.
We note finally that the statistics learning techniques can be applied after compute a first set of statistics; therefore, the learned transformation will be a transformation applied to the original set of statistics. For instance, consider our initial example from Parameters as Random Variables where we model the height of humans. The original summary statistics were defined as follows:
# define statistics
from abcpy.statistics import Identity
statistics_calculator = Identity(degree=3, cross=True)
Then we can learn the optimized summary statistics from the above list of summary statistics using the semi-automatic summary selection procedure as follows:
# Learn the optimal summary statistics using Semiautomatic summary selection
from abcpy.statisticslearning import Semiautomatic
statistics_learning = Semiautomatic([height], statistics_calculator, backend,
n_samples=1000, n_samples_per_param=1, seed=1)
# Redefine the statistics function
new_statistics_calculator = statistics_learning.get_statistics()
We remark that the minimal amount of coding needed for using the neural network based regression does not change at all:
# Learn the optimal summary statistics using SemiautomaticNN summary selection;
# we use 200 samples as a validation set for early stopping:
from abcpy.statisticslearning import SemiautomaticNN
statistics_learning = SemiautomaticNN([height], statistics_calculator, backend,
n_samples=1000, n_samples_val=200, n_epochs=20, use_tqdm=False,
n_samples_per_param=1, seed=1, early_stopping=True)
# Redefine the statistics function
new_statistics_calculator = statistics_learning.get_statistics()
And similarly for the other approaches.
We remark how abcpy.statisticslearning.SemiautomaticNN (as well as the other NN-based statistics learning approaches) allow to specify a neural network through the optional embedding_net parameter (in abcpy.statisticslearning.ExponentialFamilyScoreMatching, you analogously have simulations_net and parameters_net). According to the value given to embedding_net, different NNs are used:
- a torch.nn object can be passed to embedding_net to be used as the NN to learn summary statistics.
- Alternatively, a list with some integer numbers denoting the width of the hidden layers of a fully connected NN can be specified (with the length of the list corresponding to the number of hidden layers). In this case, the input and output sizes are determined so that things work correctly: input size correspond to the data size after the provided statistics_calculator has been applied, while output size corresponds to the number of parameters in the model. The function taking care of instantiating the NN is
abcpy.NN_utilities.networks.createDefaultNN(). - If embedding_net is not specified, the behavior is similar to the latter bullet point, but with the number of hidden sizes fixed to 3 and their width determined as:
[int(input_size * 1.5), int(input_size * 0.75 + output_size * 3), int(output_size * 5)].
The parameters simulations_net and parameters_net of abcpy.statisticslearning.ExponentialFamilyScoreMatching have a similar behavior, with the former network still taking as input the data after statistics_calculator has been applied, while the latter taking as input the parameters; additionally, here the embedding size can be chosen arbitrarily through the argument embedding_dimension, for which the default value is the number of parameters in the model. You can find more information in the docstring for abcpy.statisticslearning.ExponentialFamilyScoreMatching, or in the example in examples/statisticslearning/gaussian_statistics_learning_exponential_family.py.
We can then perform the inference as before, but the distances will be computed on the newly learned summary statistics.
The above summary statistics learning routines can also be initialized with previously generated parameter-observation pairs (this can be useful for instance when different statistics learning techniques need to be tested with the same training dataset). The abcpy.inferences.DrawFromPrior class can be used to generate such training data. We provide an example showcasing this in examples/statisticslearning/gaussian_statistics_learning_DrawFromPrior_reload_NNs.py.
Finally, when we use a neural network-based summary statistics learning approach, the neural network can be stored to disk and loaded later. This is done in the following chunk of code (taken from an example shipped with code); notice the use of the abcpy.statistics.NeuralEmbedding Statistics class:
# get the statistics from the already fit StatisticsLearning object 'semiNN':
learned_seminn_stat = semiNN.get_statistics()
# this has a save net method:
learned_seminn_stat.save_net("seminn_net.pth")
# to reload: need to use the Neural Embedding statistics fromFile; this needs to know which kind of NN it is using;
# need therefore to pass either the input/output size (it data size and number parameters) or the network class if
# that was specified explicitly in the StatisticsLearning class. Check the docstring for NeuralEmbedding.fromFile
# for more details.
from abcpy.statistics import NeuralEmbedding
learned_seminn_stat_loaded = NeuralEmbedding.fromFile("seminn_net.pth", input_size=1, output_size=2)
Model Selection¶
A further extension of the inferential problem is the selection of a model (M), given an observed
dataset, from a set of possible models. The package also includes a parallelized version of random
forest ensemble model selection algorithm [abcpy.modelselections.RandomForest].
Lets consider an array of two models Normal and StudentT. We want to find out which one of these two models are the most suitable one for the observed dataset y_obs.
# Create a array of models
from abcpy.continuousmodels import Uniform, Normal, StudentT
model_array = [None] * 2
# Model 1: Gaussian
mu1 = Uniform([[150], [200]], name='mu1')
sigma1 = Uniform([[5.0], [25.0]], name='sigma1')
model_array[0] = Normal([mu1, sigma1])
# Model 2: Student t
mu2 = Uniform([[150], [200]], name='mu2')
sigma2 = Uniform([[1], [30.0]], name='sigma2')
model_array[1] = StudentT([mu2, sigma2])
We first need to initiate the Model Selection scheme, for which we need to define the summary statistics and backend:
# define statistics
from abcpy.statistics import Identity
statistics_calculator = Identity(degree=2, cross=False)
# define backend
from abcpy.backends import BackendDummy as Backend
backend = Backend()
# Initiate the Model selection scheme
modelselection = RandomForest(model_array, statistics_calculator, backend, seed=1)
Now we can choose the most suitable model for the observed dataset y_obs,
# Choose the correct model
model = modelselection.select_model(y_obs, n_samples=100, n_samples_per_param=1, )
or compute posterior probability of each of the models given the observed dataset.
# Compute the posterior probability of the chosen model
model_prob = modelselection.posterior_probability(y_obs)
Logging¶
Sometimes, when running inference schemes it is desired to have a more verbose logging output. This can be achieved by using Python’s standard logger and setting it to info mode at the beginning of the file.
import logging
logging.basicConfig(level=logging_level)